#include "ampmarginaliser.h"

Functions
float	marginalise_amplitudes_f (int Nmodels, float *modelModel, float dataModel, float sigma, unsigned int lastHalfRange)
	The same as `marginalise_amplitudes()`, but for `float` inputs rather than `double`.
double	marginalise_amplitudes_except_final (int Nmodels, double *modelModel, double dataModel, double sigma)
	Marginalise over all amplitudes except for the final model component.
float	marginalise_amplitudes_except_final_f (int Nmodels, float *modelModel, float dataModel, float sigma)
	The same as `marginalise_amplitudes_except_final()`, but for `float` inputs rather than `double`.
double	marginalise_amplitudes_linear (int Nmodels, double modelModel[], double dataModel[], double sigma, unsigned int lastHalfRange)
	The same as `marginalise_amplitudes()`, but with the `modelModel` array made into a 1D vector rather than a 2D array.
double	marginalise_amplitudes_except_final_linear (int Nmodels, double modelModel[], double dataModel[], double sigma)
	The same as `marginalise_amplitudes_except_final()`, but with the `modelModel` array made into a 1D vector rather than a 2D array.
double	marginalise_three_amplitudes (double *modelModel, double dataModel, double sigma, unsigned int lastHalfRange)
	Performs the likelihood ratio marginalisation explicitly written out for the model amplitude components.
float	marginalise_three_amplitudes_f (float *modelModel, float dataModel, float sigma, unsigned int lastHalfRange)
	The same as `marginalise_three_amplitudes()`, but for `float` inputs rather than `double`.
double	marginalise_three_amplitudes_exclude_final (double *modelModel, double dataModel, double sigma)
	Explicitly marginalise over the first three model component amplitudes, but not the final one.

Detailed Description

Function Documentation

double marginalise_amplitudes_except_final	(	int	Nmodels,
		double **	modelModel,
		double *	dataModel,
		double	sigma
	)

Marginalise over all amplitudes except for the final model component.

This function allows for a model that contains components for which the amplitudes are required to be marginalisation over, and also a component (which could contain multiple components defined by various parameters itself) for which no marginalisation is required. It follows the same route as for marginalise_amplitudes(), but stops before the final marginalisation.

All the amplitude marginalisations are performed over the 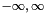${-\infty, \infty}$ range.

double marginalise_three_amplitudes	(	double **	modelModel,
		double *	dataModel,
		double	sigma,
		unsigned int	lastHalfRange
	)

Performs the likelihood ratio marginalisation explicitly written out for the model amplitude components.

For three amplitudes the marginalised likelihood ratio is given by:

$\mathcal{L} = (2\pi)^{3/2}\sigma^3 \frac{e^{-\frac{ d_h^2(f_g^2-FG) -2d_h(d_g f_g f_h - d_f f_h G -d_g F g_h + d_f f_g g_h) + d_g^2(f_h^2 - FH) + 2d_f d_g(f_g H - f_h g_h) + d_f^2(g_h^2 - GH)}{2\sigma^2 (FGH + 2f_g f_h g_h -G f_h^2 - H f_g^2 - F g_h^2) }}}{\sqrt{F}\sqrt{\frac{(FG - f_g^2)}{F}}\sqrt{\frac{FGH + 2f_g f_h g_h -G f_h^2 - F g_h^2 - H f_g^2}{FG - f_g^2}}}$

for an integral between 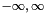${-\infty, \infty}$ for all amplitudes, and

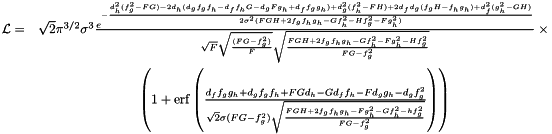
$\begin{eqnarray*} \mathcal{L} =& \sqrt{2}\pi^{3/2}\sigma^3 \frac{e^{-\frac{ d_h^2(f_g^2-FG) -2d_h(d_g f_g f_h - d_f f_h G -d_g F g_h + d_f f_g g_h) + d_g^2(f_h^2 - FH) + 2d_f d_g(f_g H - f_h g_h) + d_f^2(g_h^2 - GH)}{2\sigma^2 (FGH + 2f_g f_h g_h -G f_h^2 - H f_g^2 - F g_h^2) }}}{\sqrt{F}\sqrt{\frac{(FG - f_g^2)}{F}}\sqrt{\frac{FGH + 2f_g f_h g_h -G f_h^2 - F g_h^2 - H f_g^2}{FG - f_g^2}}} \times \\ & \left( 1 + {\rm erf}\left( \frac{d_f f_g g_h + d_g f_g f_h + FG d_h - G d_f f_h - F d_g g_h - d_g f_g^2}{\sqrt{2}\sigma(FG-f_g^2)\sqrt{\frac{FGH + 2f_g f_h g_h - F g_h^2 - G f_h^2 - h f_g^2}{FG-f_g^2}}} \right) \right) \end{eqnarray*}$

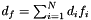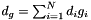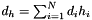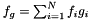
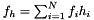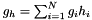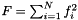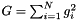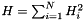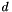for the final integral being between $[0, \infty]$ . 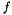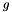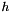In these equations we have used the following substitutions: $d_f = \sum_{i=1}^N d_i f_i$ , $d_g = \sum_{i=1}^N d_i g_i$ , $d_h = \sum_{i=1}^N d_i h_i$ , $f_g = \sum_{i=1}^N f_i g_i$ $f_h = \sum_{i=1}^N f_i h_i$ , $g_h = \sum_{i=1}^N g_i h_i$ , $F = \sum_{i=1}^N f_i^2$ , $G = \sum_{i=1}^N g_i^2$ , and $H = \sum_{i=1}^N H_i^2$ where $d$ is the data and $f$ , $g$ and $h$ are the three model components for which the amplitudes have been marginalised over.

This function explicitly writes out the marginalised likelihood ratio for a model consisting of three components with the amplitudes marginalised over. This can be used to test the correctness of the marginalise_amplitudes() function.

double marginalise_three_amplitudes_exclude_final	(	double **	modelModel,
		double *	dataModel,
		double	sigma
	)

Explicitly marginalise over the first three model component amplitudes, but not the final one.

This function uses the fully expanded integral over the amplitudes of first three components of a signal model, whilst not integrating over the final fourth component's amplitude. All the amplitude marginalisations are performed over the 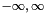${-\infty, \infty}$ range. This can be used to test the correctness of the marginalise_amplitudes_except_final() function.

Functions

Detailed Description

Function Documentation